円周上にn個の点をとり、それらを直線で結んで円を分けてできる領域の個数の数列は?

つづいて、次の問題はどう考えたらよいだろうか。

(円周上にn個の点をとりそれらを直線で結んで円を分けてできる領域の個数の数列)
円を1つ考えます。nを1以上の整数として、この円の円周上にn個の点をとります。それをすべて直線で結びます。3つ以上の線が1つの点で交わることはないような場合を考えます。円はいくつかの領域に分けられます。その領域の個数を並べた数列を考えます。
初項、第2項、第3項、第4項、第5項の順に並べると、1, 2, 4, 8, 16となります。
それでは、この数列 (1, 2, 4, 8, 16, 〇, …) の第6項 〇 に入る数は何でしょうか?

数列の話をしていたかと思えば、突然、円が出てきて「いったい何だ、これは!」という感じを持たれたかもしれない。
唐突なシーンチェンジで読者の皆さんを驚かせたとしたら、大変、申し訳ない。

さて、この数列も文章だけでは、ピンとこないだろう。試しにいくつか描いてみると理解しやすい。

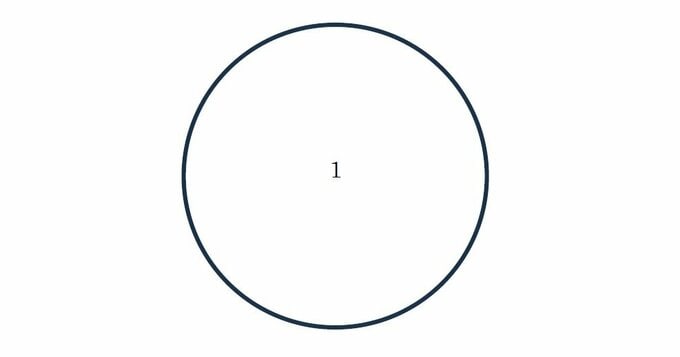
n=1のとき、円周上に1個だけ点をとっても直線で結ぶことはできない。領域は円全体の1個だ。

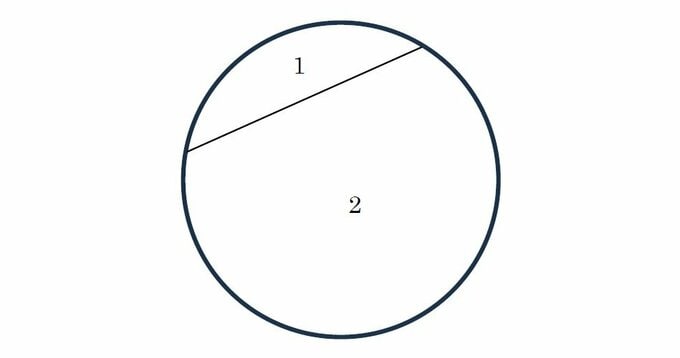
n=2のとき、円周上に2個点をとると直線1本で結ぶことができる。円はこの直線で2つに分かれるので、領域の個数は2個だ。

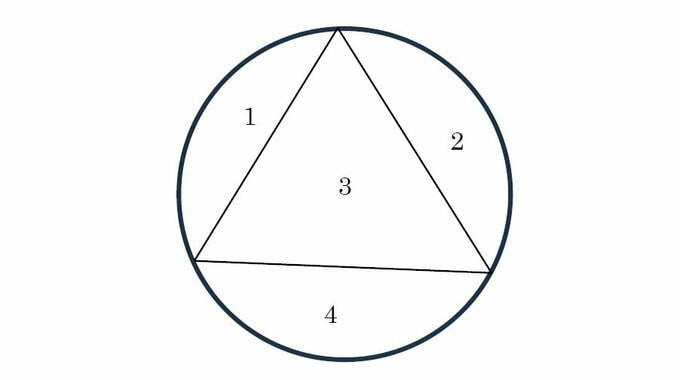
n=3のとき、円周上に3個点をとるとそれらを直線で結んで円に内接する三角形ができる。その三角形の外側に3つ、内側に1つで、領域の個数は4個となる。

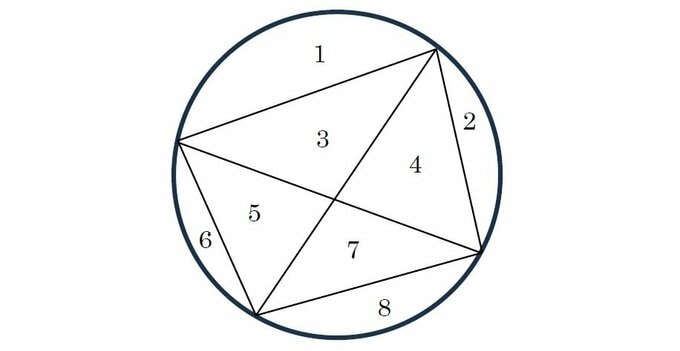
n=4のとき、円周上に4個点をとるとそれらを直線で結んで、領域の個数は8個となる。

n=5のとき、円周上に5個点をとるとそれらを直線で結んで、領域の個数は16個となる。

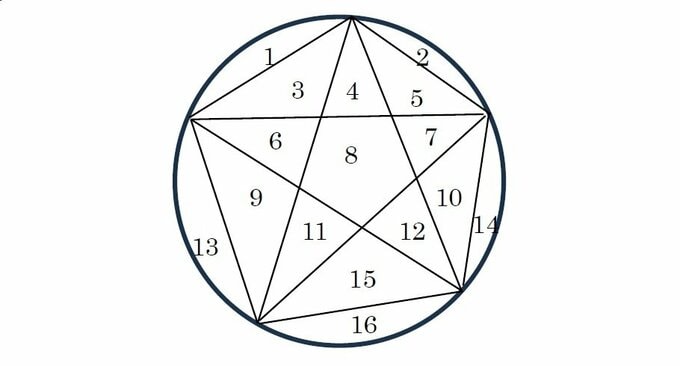
確かに、問題文に示されている通り、1, 2, 4, 8, 16という数列になっている。

それでは、〇に入るのは何だろうか。
ここで、「今度こそ、初項1、公比2の等比数列と同じなのではないか」という気がするか。
それとも「どうせまた、第6項でそれまでの項と違った増え方をするのだろう」と思うか。
なかなか予想はしづらいところだ。

そこで、n=6のとき、円周上に6個点をとって、それらを直線で結んでみる。

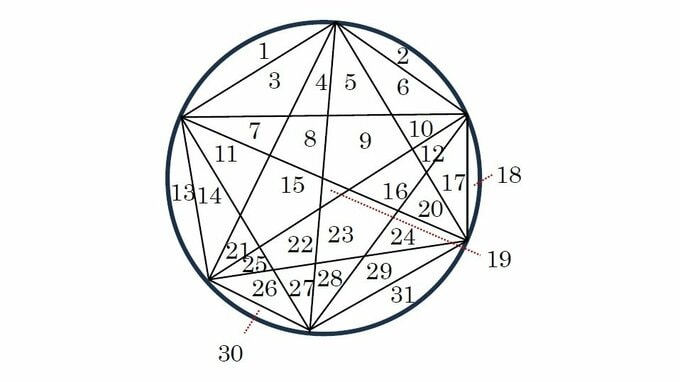
円を分けてできた領域の数は、31個。〇に入る数は、31となる。

円周上にn個の点をとり、それらを直線で結んで円を分けてできる領域の個数の数列は、1, 2, 4, 8, 16, 31, 57, 99, 163, 256, 386, 562, 794, 1093, 1471, 1941, …と続いていく。初項1、公比2の等比数列や、nの階乗の約数の個数の数列とは異なる形で、増加していく。

この数列は「モーザーの円の最大分割問題」の答えとして知られているもので、第n項は、

(n^4 － 6n^3 ＋ 23n^2 － 18n ＋ 24)/24

となる。

(本稿ではその証明は割愛する。気になる方は、“Moser's circle problem”等のキーワードでネット検索をしていただきたい。)